Se você ainda não viu, confira a série da Netflix, A Era dos Dados (Connected). É uma boa série. O apresentador, Latif Nasser, discute vários assuntos da ciência popular. A Netflix a promove como uma série “que investiga as surpreendentes e complicadas formas pelas quais estamos conectados uns aos outros, ao mundo e ao universo.” [1]
No quarto episódio, intitulado “Dígitos” (“Numbers”), Latif explora a Lei de Benford (BL), também conhecida como Lei do Primeiro Dígito. É uma observação de que muitos conjuntos de dados, tanto criados pelo homem quanto da natureza, contêm mais dígitos que começam com o número 1 do que qualquer outro dígito, cerca de 30% de todos os números. E os dígitos iniciais subsequentes diminuem de frequência até o número 9, que aparece como o primeiro dígito em apenas cerca de 5% dos números nos conjuntos de dados. Isso é surpreendente, pois se esperaria que a distribuição dos nove dígitos possíveis dos números fosse distribuída uniformemente em cerca de 11% cada.
A série olha para a história da BL e mostra que conjuntos de dados tão variados como o tamanho dos vulcões, o comprimento combinado das notas na música clássica e as demonstrações financeiras das empresas parecem seguir a BL.
Há uma pergunta que foi feita, mas nunca realmente respondida – por que muitos conjuntos de dados seguem a BL? A série sugere que a existência da BL revela algum tipo de esquema cósmico profundo do universo.
Aqui está uma explicação simples que nunca foi mencionada por Nasser, nem por ninguém com quem ele entrevistou:
Conjuntos de dados compostos por números que são produtos de múltiplos fatores independentes tendem a seguir a Lei de Benford.
Essa explicação é conhecida há algum tempo [2][3][4], mas não foi incluída na série. A Lei de Benford não é uma propriedade misteriosa do nosso universo. É apenas matemática básica.
Resumo
Neste artigo, abordarei um breve histórico da BL, explicarei dois conceitos-chave: distribuições normais e logaritmos, mostrarei como um exercício de rolagem de dados pode levar à BL e, finalmente, dar uma olhada em alguns conjuntos de dados reais para ver se essa explicação se sustenta.
Contexto
A Lei de Benford recebeu o nome do físico americano Frank Benford, que publicou um artigo em 1938 chamado “The Law of Anomalous Numbers”, que descreve as frequências dos primeiros dígitos dos números observados em um conjuntos de dados [5]. Observe que este fenômeno havia sido previamente observado e publicado pelo astrônomo canadense Simon Newcomb em 1881 [6].

Nota: é comum o fato de as coisas receberem o nome de alguém que não a descobriu primeiro. Na verdade, há um nome para isso, a Lei de Epônimo de Stigler. Foi proposta pelo professor de estatística americano Stephen Stigler em 1980 quando ele escreveu que nenhuma descoberta científica leva o nome de seu descobridor original [7]. Em uma reviravolta irônica, Stigler reconheceu que o sociólogo americano Robert Merton havia previamente descoberto a “lei de Stigler”.
Voltando a Benford. Ele observou em seu artigo que muitos conjuntos de dados diversos aderiam de perto à seguinte distribuição de primeiros dígitos, mostrada como porcentagens no gráfico abaixo:
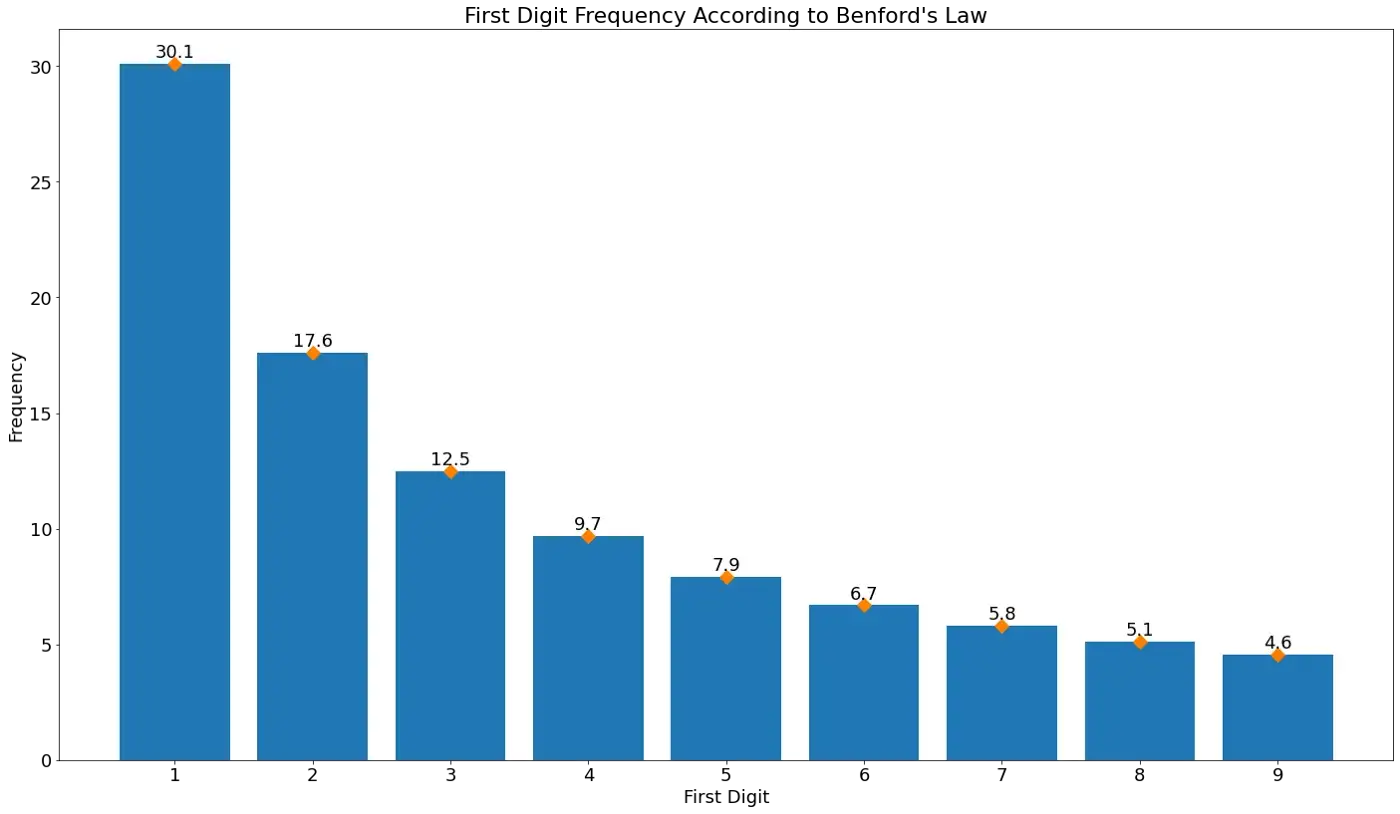
Os conjuntos de dados que Benford examinou incluíam coisas tão diversas como as populações das cidades, pesos atômicos de compostos, despesas financeiras e até mesmo todos os números que ele poderia encontrar em um jornal específico. Aqui está um trecho de sua carta.
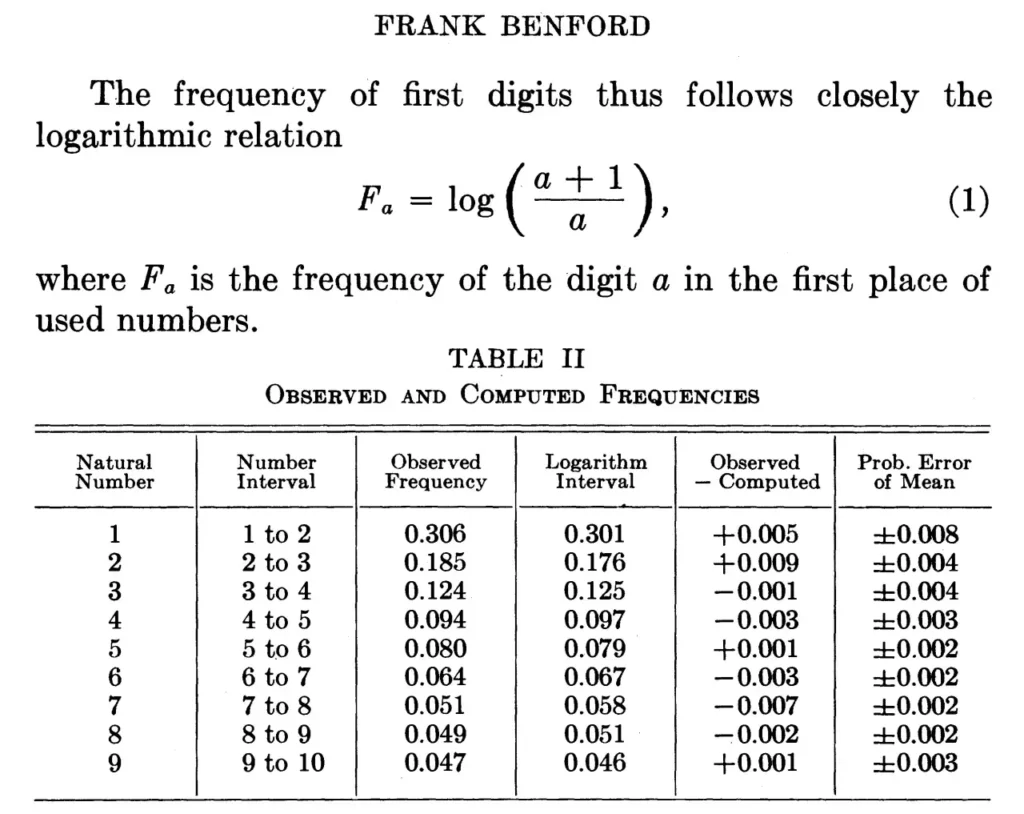
Ele continua explicando sua lei de frequência observada do primeiro dígito em termos matemáticos, mas não apresenta uma razão para isso. Ele escreve que a lei “evidentemente vai mais fundo entre as raízes das causas primordiais do que nosso sistema numérico sozinho pode explicar”. [5]
A seguir, vamos aprender sobre distribuições normais observando as velocidades de tráfego nas rodovias:

Distribuições Normais
Você provavelmente já viu como uma distribuição normal se parece. É a famosa “curva do sino” da teoria da probabilidade. Uma distribuição normal, também conhecida como distribuição Gaussiana, é um tipo de distribuição de probabilidade contínua para uma variável.
Por exemplo, imagine que os planejadores de uma cidade queiram verificar a velocidade média de um ponto específico em uma rodovia. Eles colocam uma par de tiras de sensor na estrada e começam a registrar as velocidades dos carros que passam. Dê uma olhada nos dados de amostra abaixo em um histograma:
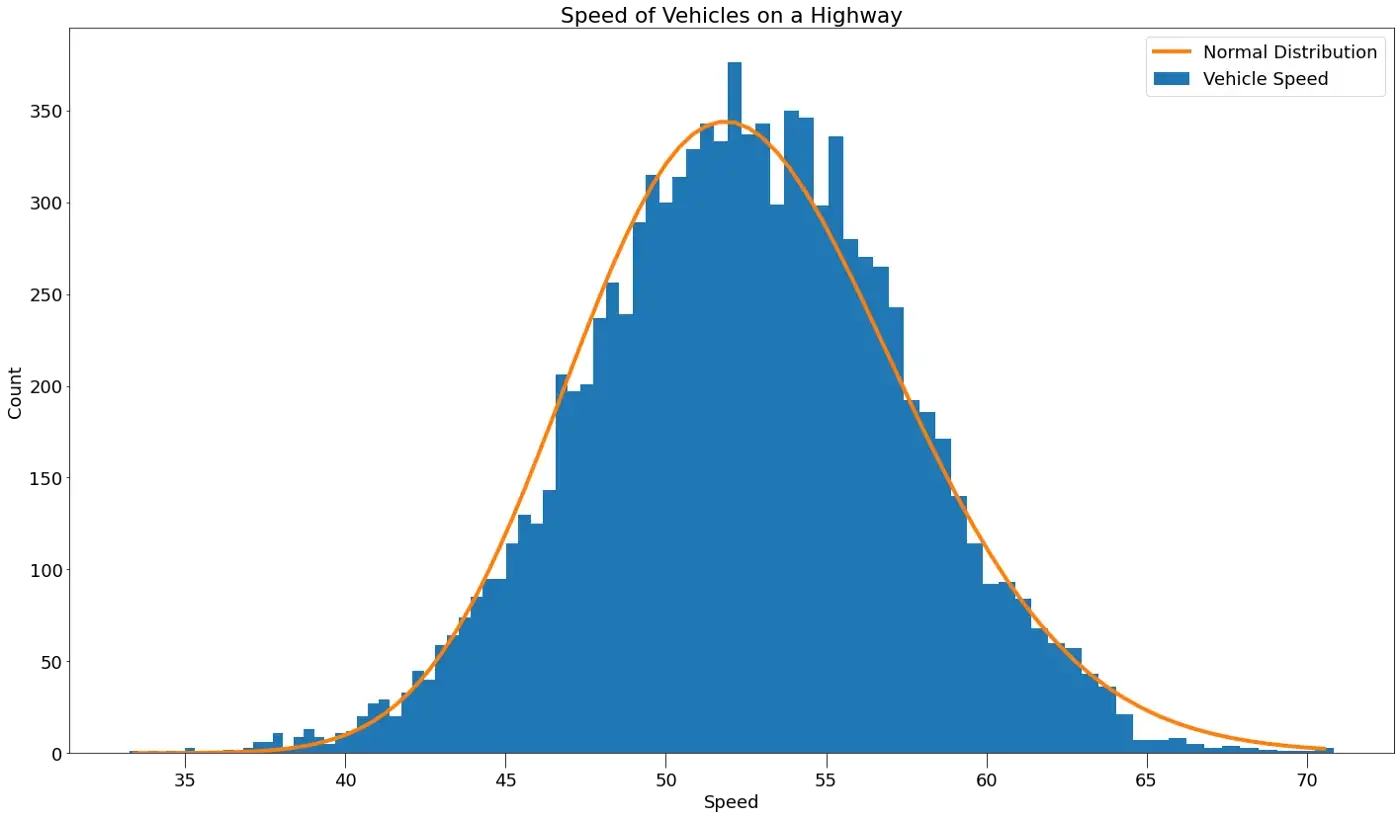
A velocidade média dos veículos é de cerca de 52 milhas por hora e a maioria dos viajantes vai entre 45 e 60 milhas por hora. Há algumas exceções. Pelo menos um carro estava andando a 35 milhas por hora e outro carro estava correndo acima de 70 milhas por hora.
Logaritmos
O segundo conceito-chave é entender como os logaritmos funcionam. Um logaritmo é uma função inversa da exponenciação. Para esta discussão, vamos nos ater aos logaritmos base 10, embora existam outros. Por exemplo, se elevarmos 10 na quinta potência, obtemos 100.000 (um dígito inicial com cinco zeros). Então, o log de 100.000 nos dá 5. E o log de 10.000 nos dá 4. Você entendeu a ideia.
Os logaritmos são úteis para observar os dados em que os valores próximos de zero estão agrupados, mas os valores mais altos estão mais espalhados. Considere os dois gráficos abaixo:


Ambos os gráficos mostram os mesmos dados em diferentes escalas horizontais. O gráfico superior mostra os pontos de dados em um eixo linear e o gráfico inferior mostra os pontos de dados em um eixo logarítmico.
Observe como os pontos de dados na escala log estão mais uniformemente distribuídos. Também no gráfico inferior, observe como os intervalos entre os números com um dígito inicial de um são muito maiores do que os outros intervalos.
Vou te contar um pouco mais sobre esses intervalos na seção a seguir, na qual faremos três simulações de lançamento de dados.

Uma Jogada de Dados
Para uma compreensão de como as distribuições seguem a BL, vamos dar uma olhada em três simulações usando jogadas de de dados.
Imagine que você está fazendo de uma grande aula de estatística online. São 10.000 alunos. O professor pede para cada aluno que jogue um dado de seis lados e insira o resultado em uma planilha. Aqui está um histograma dos resultados:
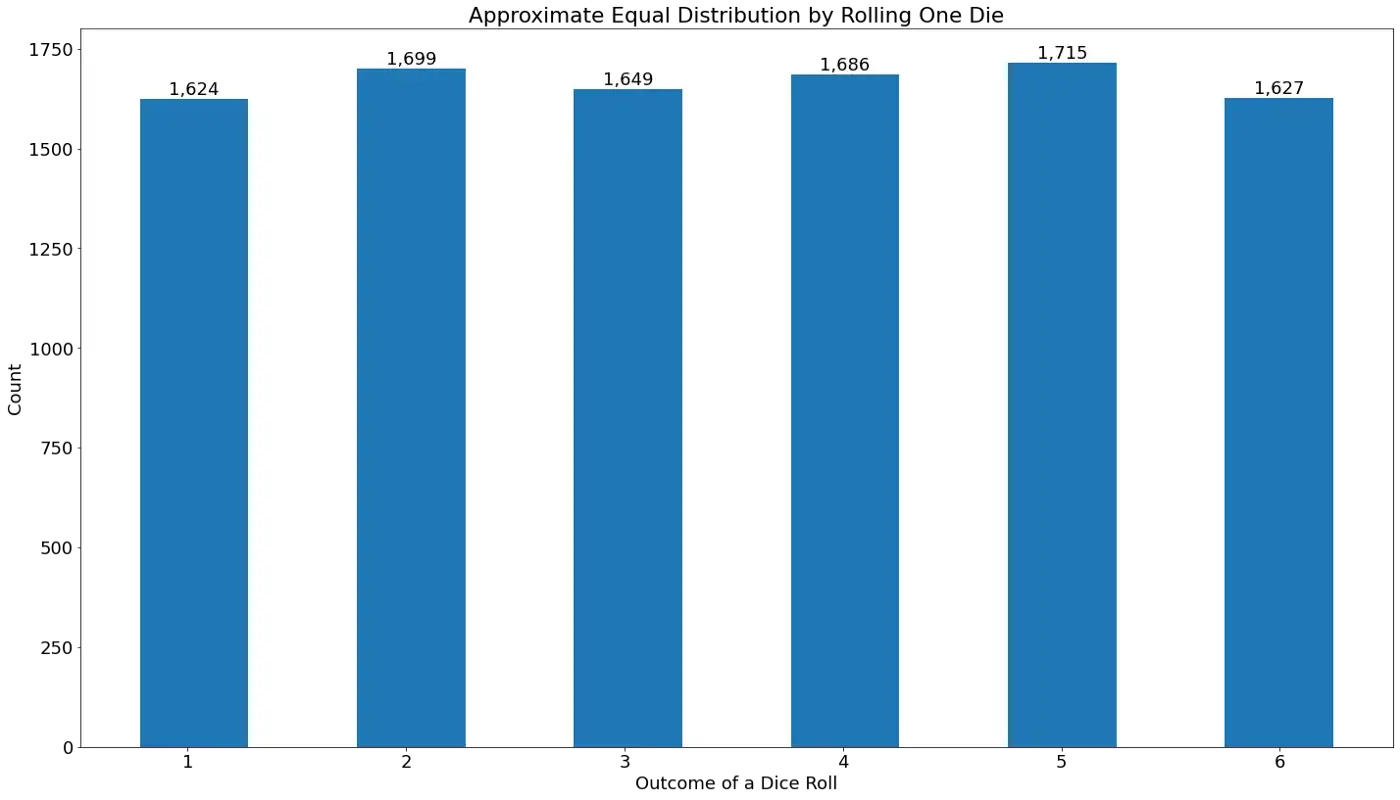
Com 10.000 lançamentos e seis resultados possíveis para cada lançamento, o resultado esperado seria de cerca de 1.666 lançamentos por resultado. Os resultados acima são próximos disso, variando de 1.624 para o número 1, a até 1.714 para o número 5. Essa é uma aproximação de uma distribuição uniforme.
Resumindo as jogadas de dados
Para o próximo exercício, o professor pede a cada aluno que jogue seu dado 100 vezes e faça uma soma. A soma para cada aluno é de aproximadamente 350. Isso ocorre porque 3,5 é a metade entre 1 e 6, e cada um deles realizou 100 jogadas. Você pode ver os resultados no histograma abaixo:
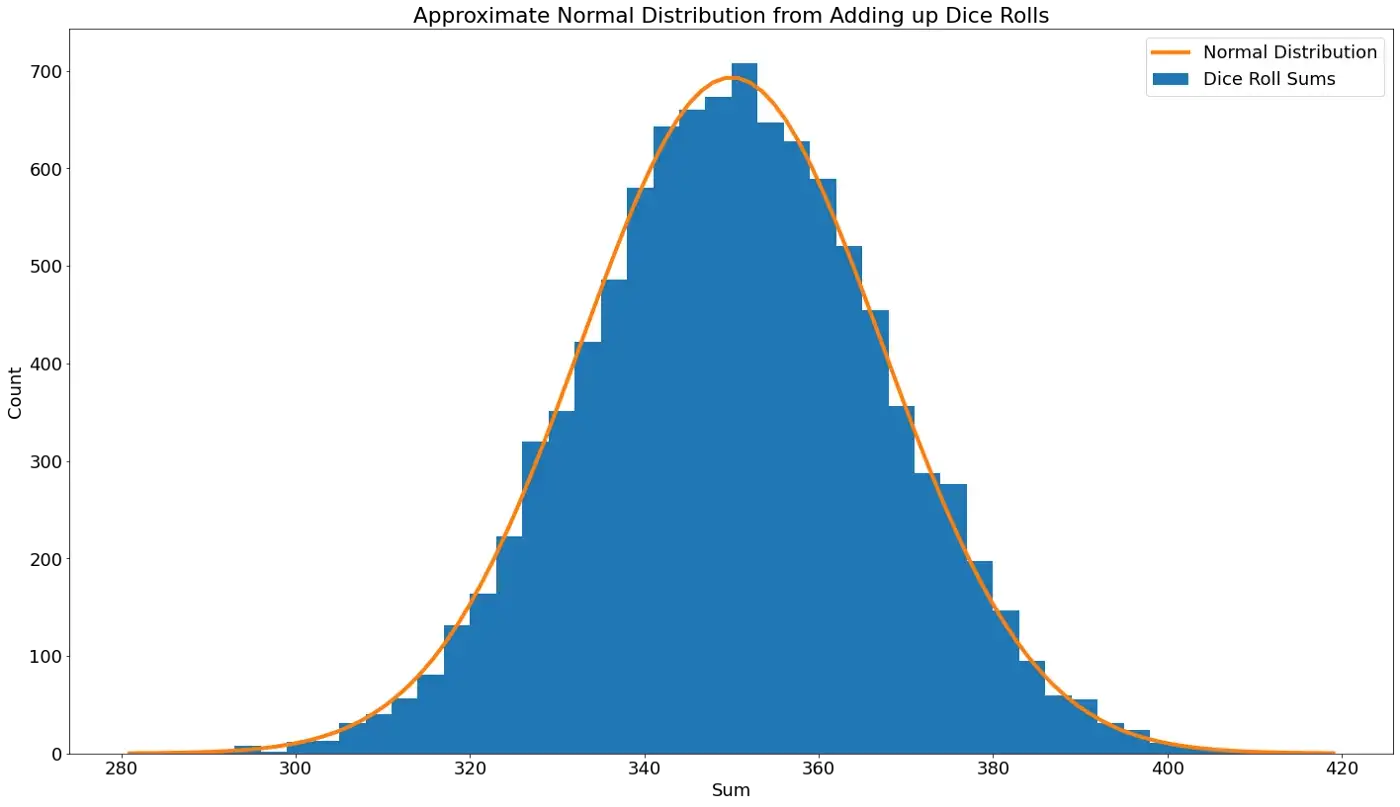
Aí está nossa distribuição normal novamente. Alguns alunos obtiveram um resultado baixo que foi abaixo de 300, e alguns obtiveram um resultado alto que foi acima de 400, mas a maioria ficou na faixa de 330 a 370.
Por que obtemos uma curva de sino como resultado? O Teorema do Limite Central (CLT) da teoria da probabilidade afirma que a soma de variáveis aleatórias independentes tenderá a uma distribuição normal [4].
Multiplicando as jogadas de dados
Para o terceiro e último exercício, o professor pede a cada um dos alunos que jogue o dado novamente, mas apenas 15 vezes e depois multiplique cada número. Os produtos ficam bem grandes. A média é de cerca de 76 bilhões. O histograma mostra os resultados abaixo, mas desta vez, o eixo horizontal está usando uma escala logarítmica:
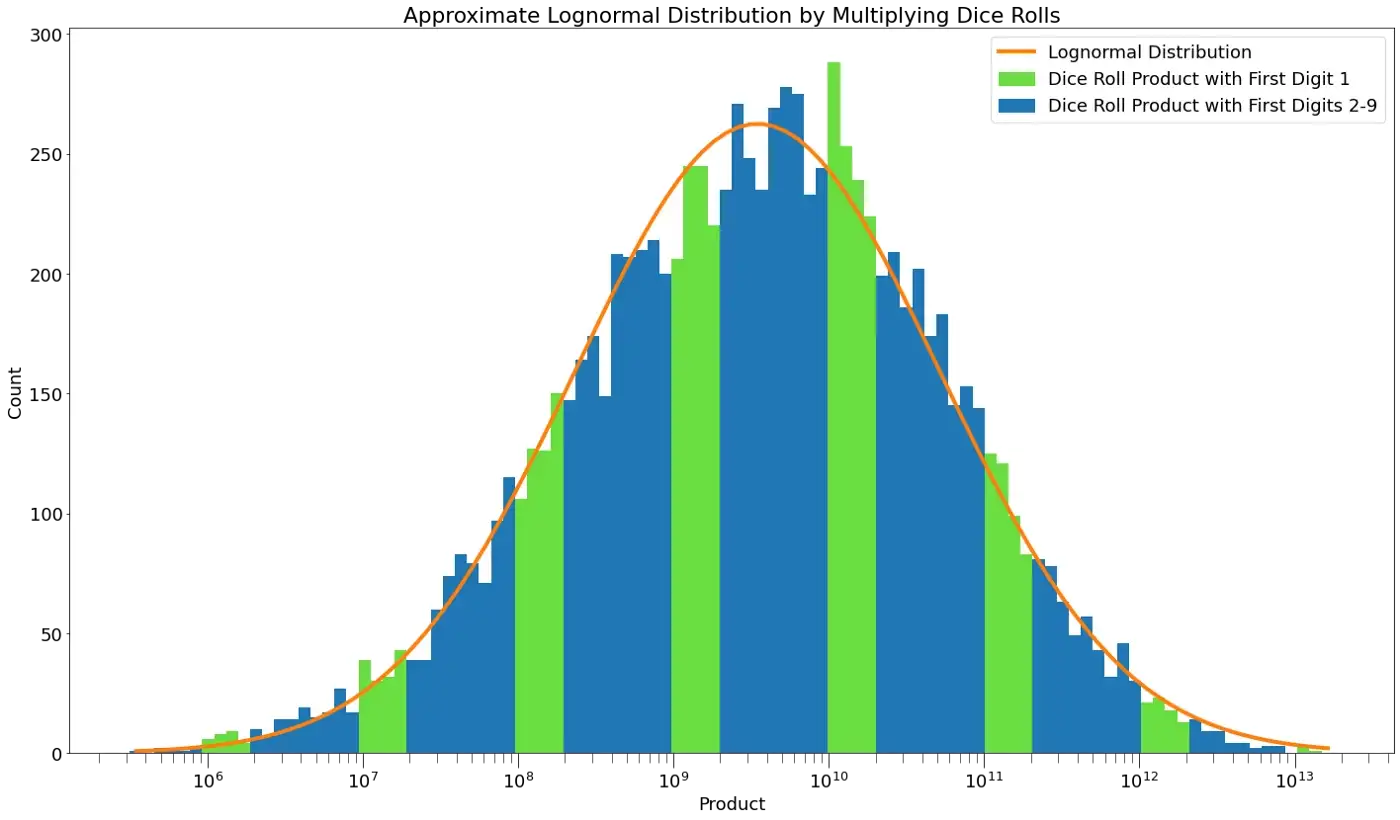
Mais uma vez, vemos nossa distribuição normal. Mas, como o eixo x está em uma escala logarítmica, a distribuição é chamada de log-normal. Por que obtemos essa distribuição? O Teorema do Limite Central Multiplicativo (MCLT) afirma que a multiplicação de variáveis aleatórias independentes tenderá a uma distribuição log-normal [4].
Observe que o eixo x do histograma acima usa potências de 10 para as marcas. Os resultados variam de um milhão (10⁶) a 10 trilhões (10¹³). Vamos dar uma olhada mais de perto no intervalo no eixo x entre 10⁹ e 10¹⁰.

Você pode ver que a grande faixa verde abrange cerca de 30% do segmento, e os 8 intervalos seguintes entre as marcas diminuem de tamanho da esquerda para a direita até que a próxima faixa verde comece. Na verdade, os segmentos são exatamente do tamanho dos intervalos definidos pela BL.

Como a distribuição no histograma é algo contínua (seguindo aproximadamente uma linha suave) e abrange muitas ordens de grandeza (com sete faixas), seria razoável pensar que os números neste exemplo estarão em conformidade com a BL. Os números caem em baldes do tamanho de Benford.
Esta observação é abordada no artigo de R. M. Fewster, “A Simple Explanation of Benford’s Law”. Ele o relaciona com um chapéu com listras. Na analogia, o chapéu representa uma distribuição log-normal de números, a borda representa o eixo x e as faixas representam a área de 30,1% que possui dígitos que começam com 1. Se as faixas cobrirem uma proporção da borda, elas cobrirão aproximadamente a mesma proporção de todo o chapéu, com faixas suficientes [8].
Vamos dar uma olhada na frequência dos dígitos iniciais para nosso terceiro exercício de lançamento de dados.
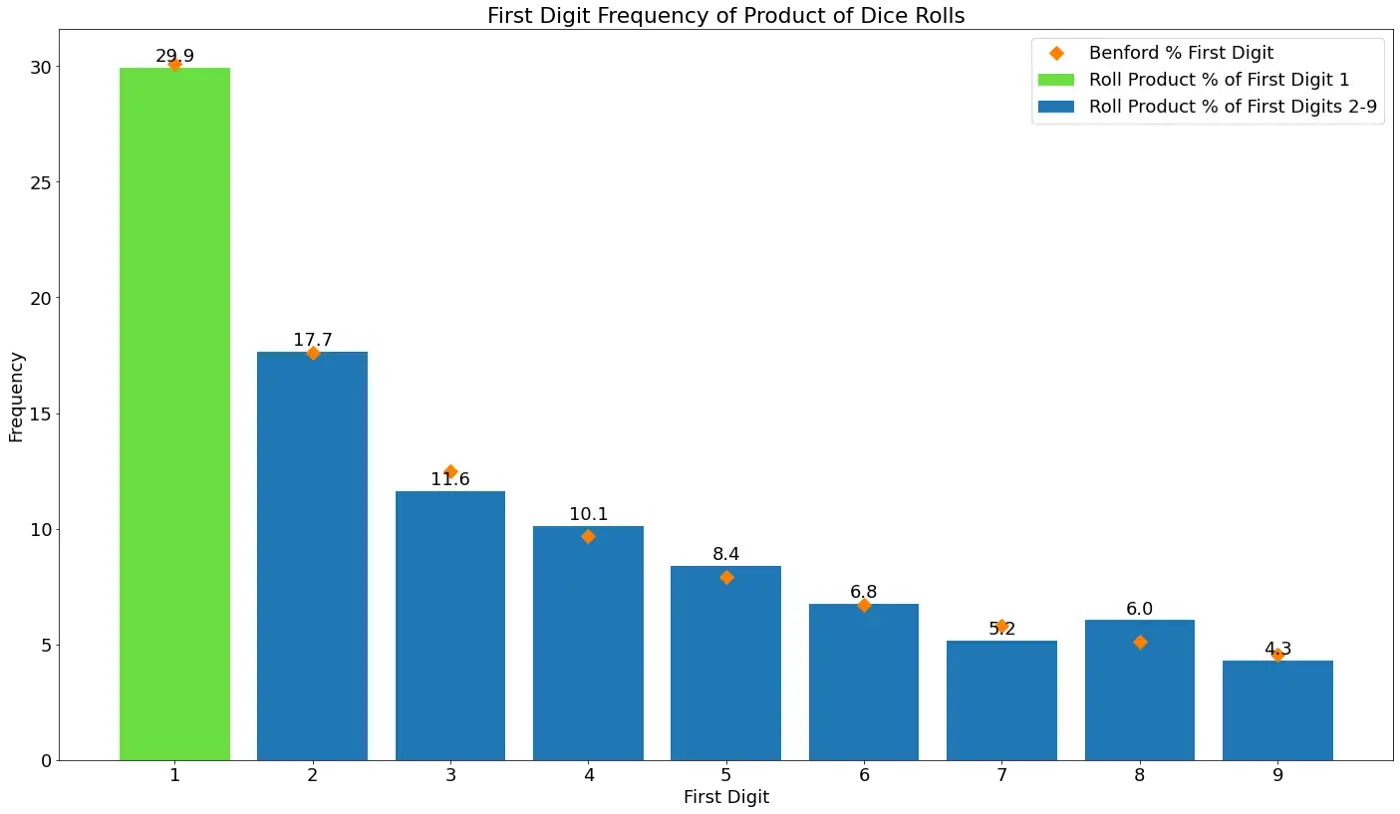
De fato, a frequência dos dígitos iniciais alinha-se razoavelmente bem com as previsões de Benford (os losangos laranja). Se rodarmos a simulação com mais produtos e/ou mais alunos, os resultados estariam ainda mais próximos das previsões.
Observe que nem todos os conjuntos de dados com distribuições log-normais estão em conformidade com a BL. As restrições são especificadas no artigo “Benford’s Law: An Empirical Investigation and a Novel Explanation”, de Paul D. Scott e Maria Fasli, da Universidade de Essex [2].
“Os dados cujas distribuições estão em conformidade com uma distribuição log-normal cujo [desvio padrão] excede 1,2 devem dar origem a distribuições de dígitos iniciais que satisfaçam a lei [de Benford]. Os dados que são propensos a satisfazer este critério devem:
(1) Ter apenas valores positivos;
(2) Ter uma distribuição unimodal cujo valor modal não seja zero;
(3) Ter uma distribuição assimétrica positiva na qual a mediana não é superior à metade da média.”– Paul D. Scott e Maria Fasli
Por outro lado, nem todos os conjuntos de dados em conformidade com a BL têm distribuições log-normais. Este fato é abordado por Anro Berger e Ted Hill em seu livro, “A basic theory of Benford’s Law” [3]. Por exemplo, eles mencionam que combinar conjuntos de dados independentes resultará em conformidade com a BL.
A seguir, veremos alguns conjuntos de dados do mundo real.

Populações de cidades e municípios
Um dos conjuntos de dados “propaganda” que segue de perto a BL são as populações de cidades. Não importa se você olha para cidades, municípios estados ou países, desde que você tenha centenas de pontos de dados que abrangem várias ordens de magnitude, os dados parecem se alinhar bem com a Lei de Benford.
Abaixo está um conjunto de dados de cidades e municípios dos EUA a partir do Censo dos EUA de 2010 [9]. Ela varia de cidades com uma população de uma pessoa, como Chesterfield, Indiana, a grandes cidades com 3,7 milhões de pessoas, como Los Angeles.
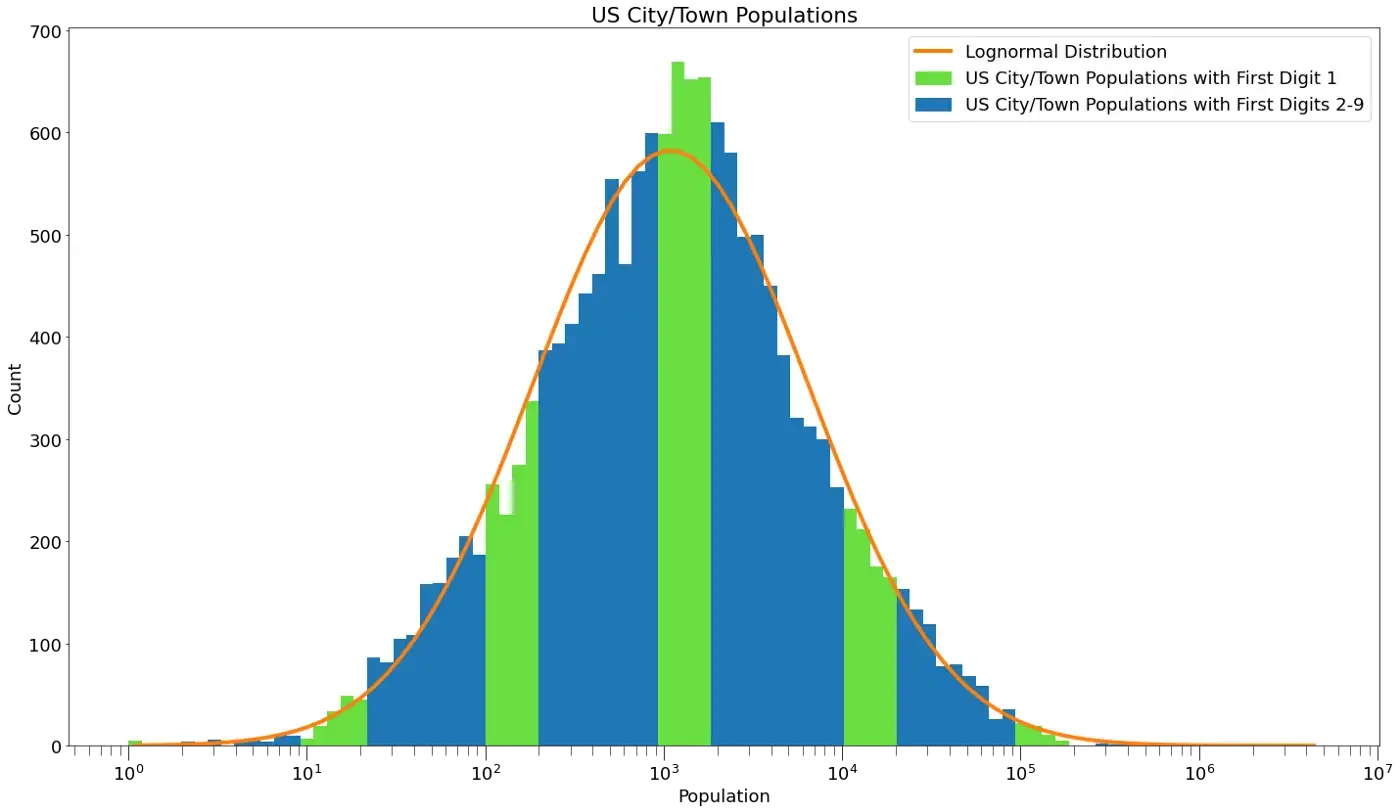
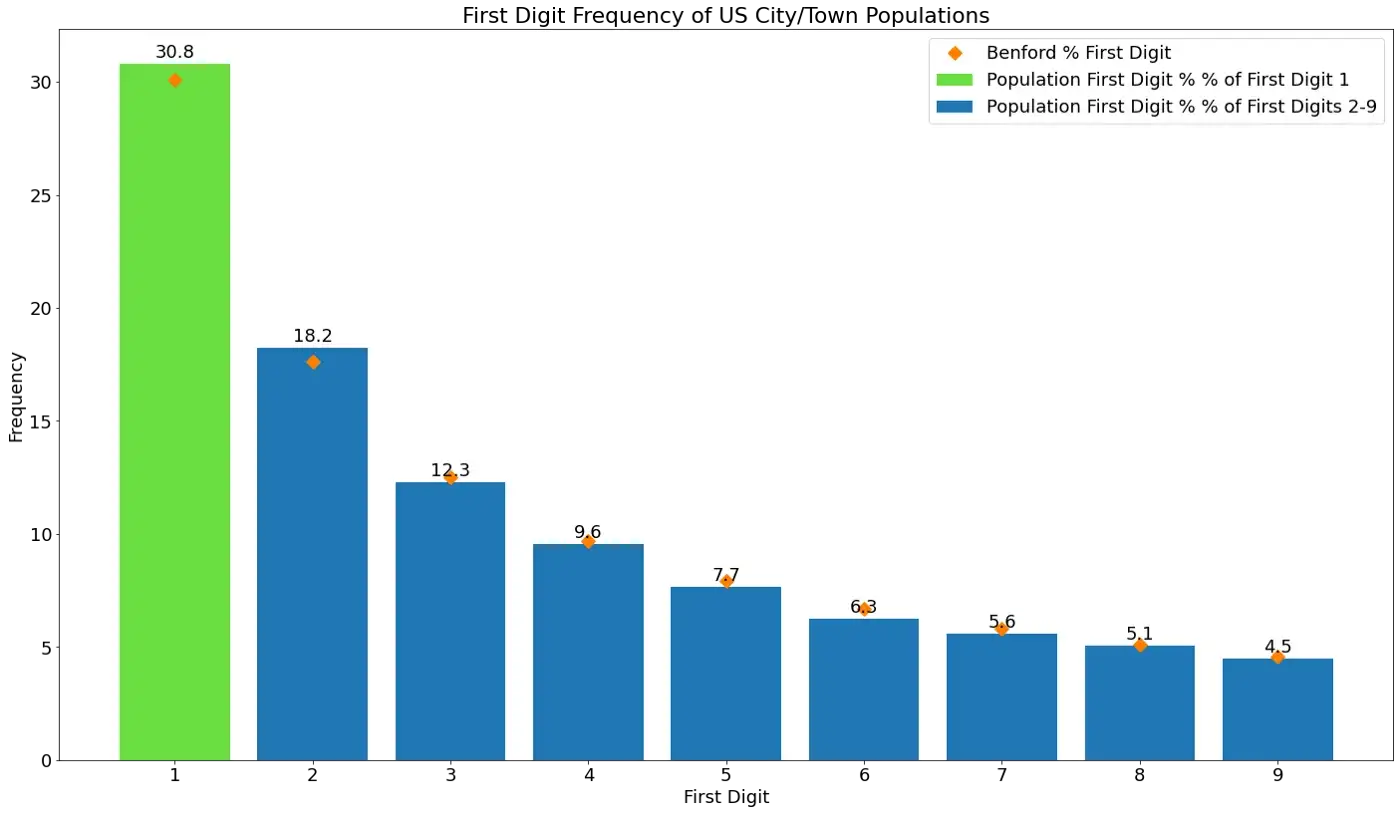
A distribuição é claramente log-normal e os primeiros dígitos seguem a Lei de Benford de perto.
Por que as populações de cidades/municípios têm uma distribuição log-normal? Minha primeira ideia é que pode haver vários fatores independentes em jogo aqui. Por exemplo, as cidades têm diferentes áreas, densidades de unidades habitacionais e números de residentes por unidade habitacional. Multiplicar esses, e talvez outros fatores juntos, pode levar a uma distribuição log-normal.
A distribuição das populações de cidades tem sido estudadas. Por exemplo, há um artigo de Ethan Decker, et al., intitulado “Global patterns of city size Distributions and their fundamental drivers” [10].
“Aqui mostramos que as distribuições nacionais, regionais e continentais do tamanho da cidade, seja com base em dados do censo ou inferidas a partir de áreas de aglomerados de luzes noturnas detectadas remotamente, são de fato distribuídas log-normalmente pela maioria das cidades … Para explorar os processos de geração, utilizamos um modelo simples que incorpora apenas duas dinâmicas humanas básicas: migração e reprodução…”
Ethan Decker, et al.
Ok, parece ser uma coisa de crescimento. Agora, vamos explorar mais da temática de finanças.

Finanças
Muitos conjuntos de dados no mundo das finanças parecem seguir a Lei de Benford. Os profissionais podem usar esse fato para ajudar a detectar fraudes e outras irregularidades.
“Constatou-se que a Lei de Benford se aplica a muitos conjuntos de dados financeiros, incluindo dados de imposto de renda ou bolsa de valores, despesas corporativas e dados de vendas, demografia e dados científicos.” [11]
– Mark Nigrini
O gráfico abaixo mostra todas as despesas que o Estado de Oklahoma pagou em 2019 [12]:
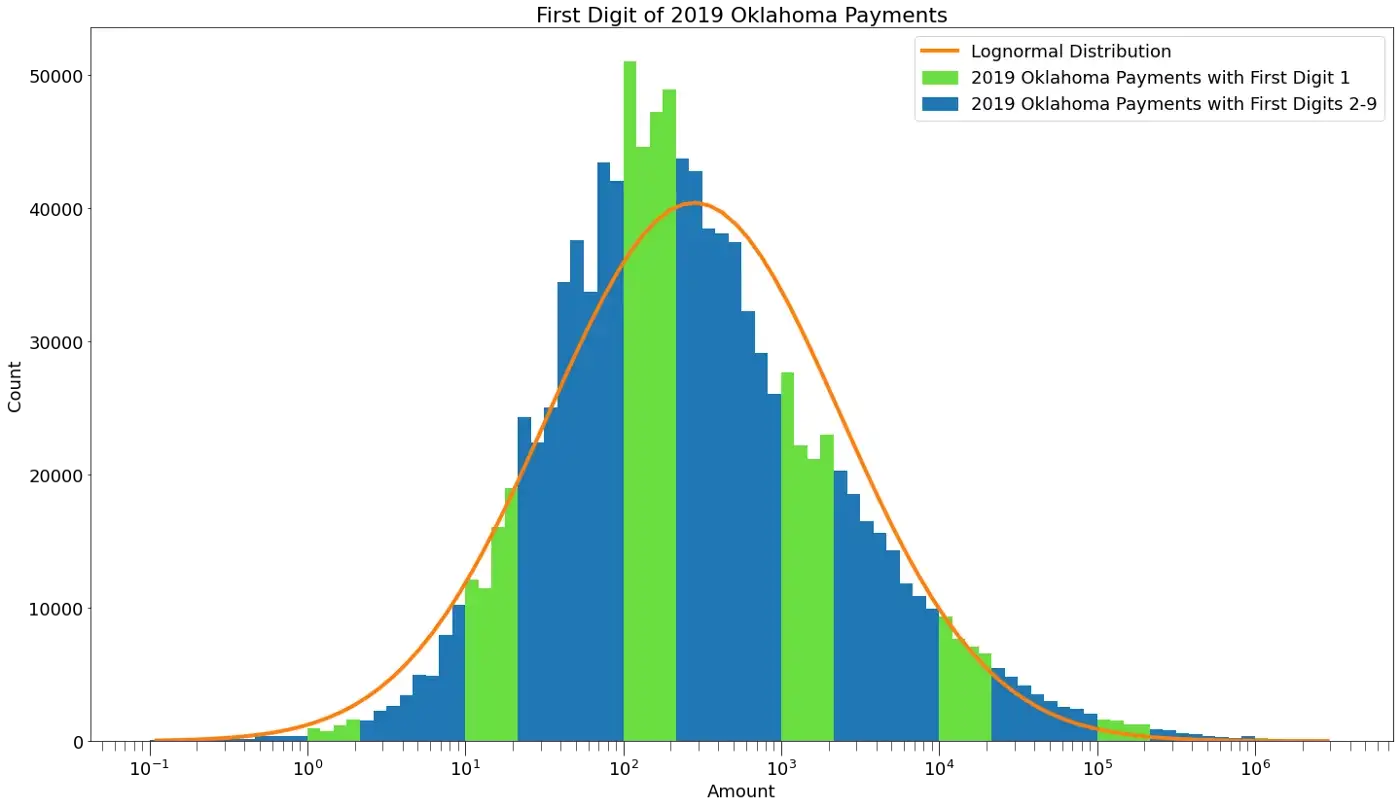
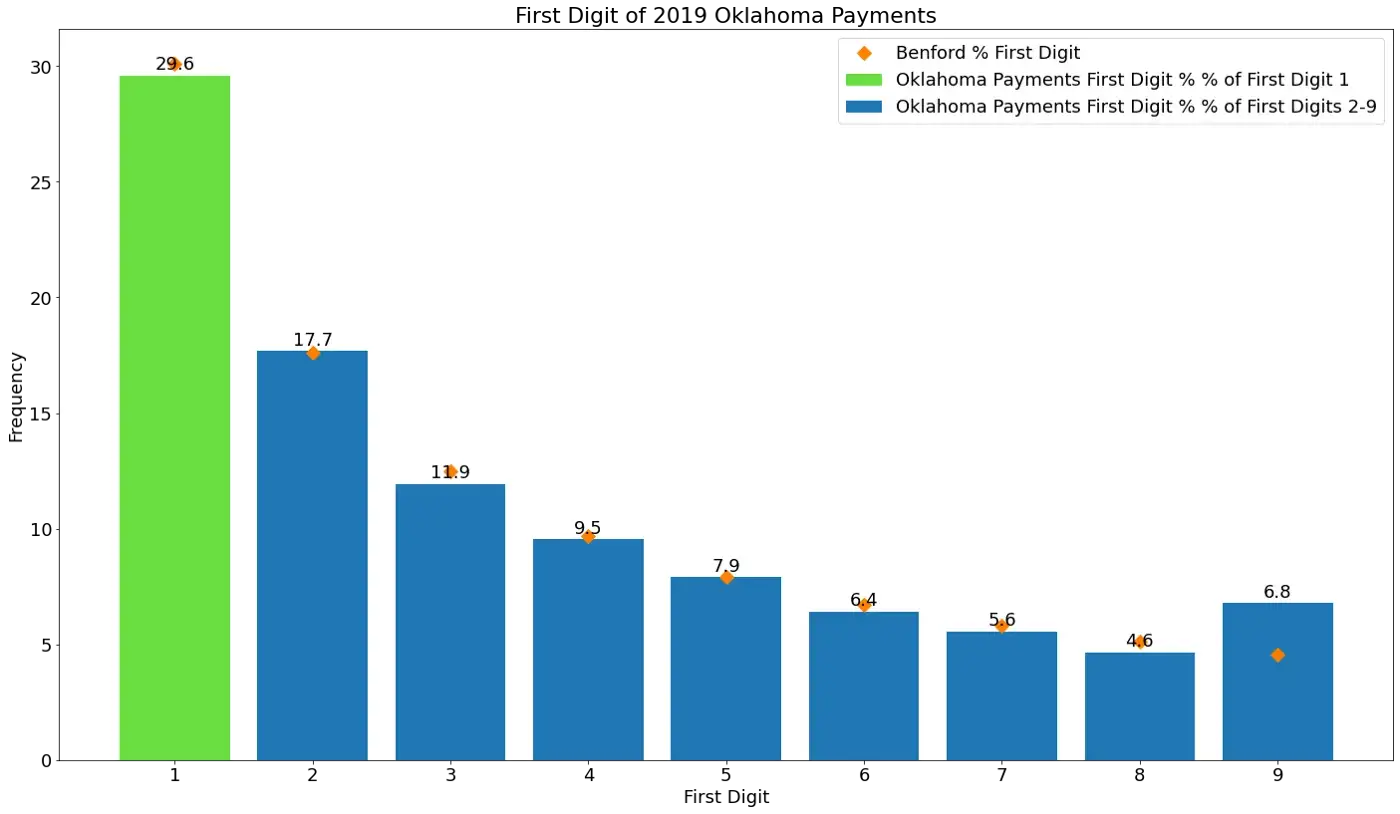
Você pode ver que há uma distribuição log-normal, mas ela está um pouco inclinada para a esquerda. Além disso, os primeiros dígitos se desviam um pouco da BL. Por exemplo, os números que começam com o dígito 9 parecem não estar em conformidade. Não está claro se esta análise mostra um problema com os livros/contas. Vou deixar para os auditores darem uma olhada mais de perto.
Há um bom artigo sobre este assunto escrito por Cindy Durtschi, et al., intitulado “The effective use of Benford’s law to assist in detecting frauding in accounting data” [12]. O artigo tem uma tabela que mostra os tipos de dados financeiros que se espera que sigam a Lei de Benford.
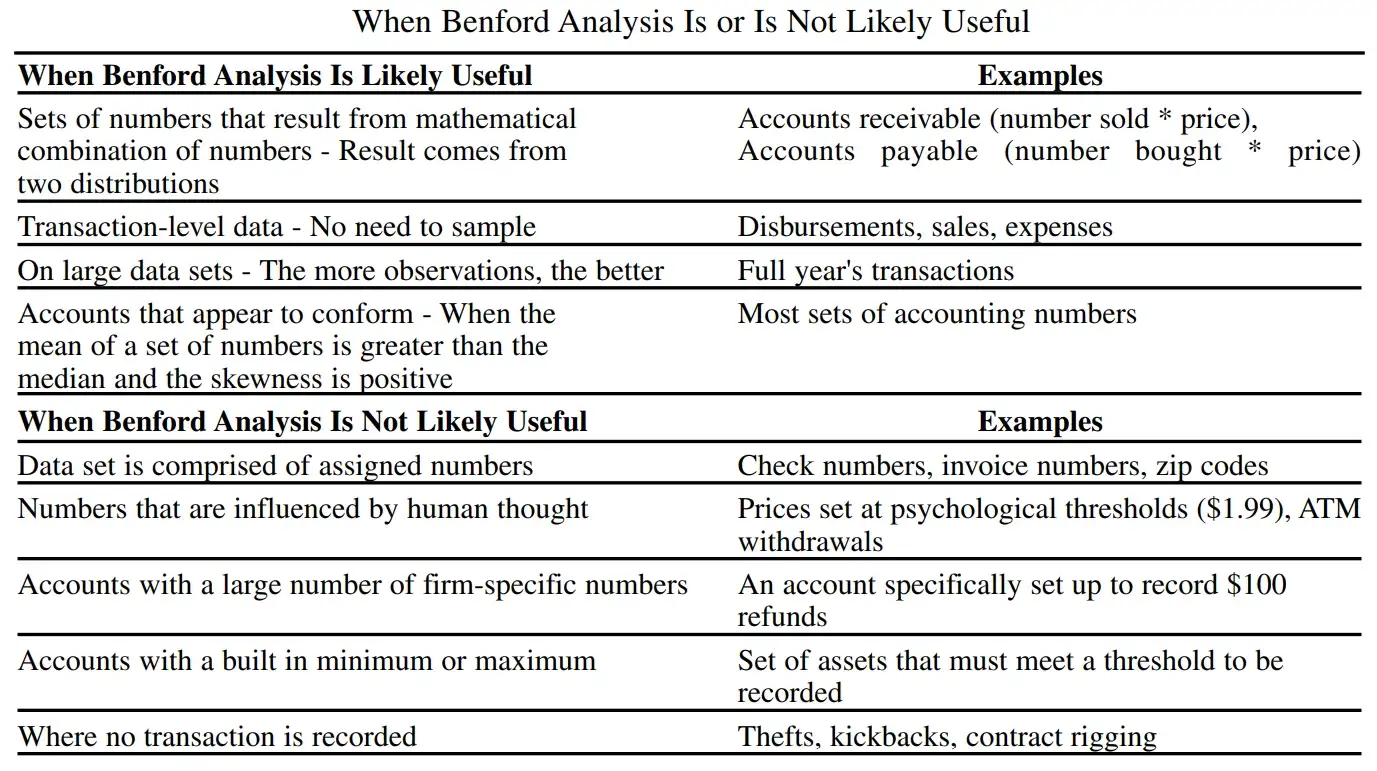
Perceba que os dois primeiros exemplos de quando a análise de Benford é provavelmente útil são o número vendido * preço e número comprado * preço. Estes valores são produtos de fatores independentes. Outros fatores multiplicativos para estes tipos de valores podem incluir impostos e taxas percentuais. Isto provavelmente faria com que os dados desta conta seguissem uma distribuição log-normal se os valores abrangessem várias ordens de grandeza.
Vejamos a seguir algo da natureza: a extensão dos rios.

Nos exemplos anteriores, vimos conjuntos de dados que têm uma distribuição log-normal e seguem a Lei de Benford que são compostos de coisas determinadas pelos seres humanos: populações de cidades/municípios e itens financeiros. Mas estes tipos de conjuntos de dados também podem ser encontrados na natureza, com pouco ou nenhum envolvimento humano. Por exemplo, vamos dar uma olhada na extensão dos rios no estado de Nova York, a partir dos dados disponíveis em data.ny.gov.
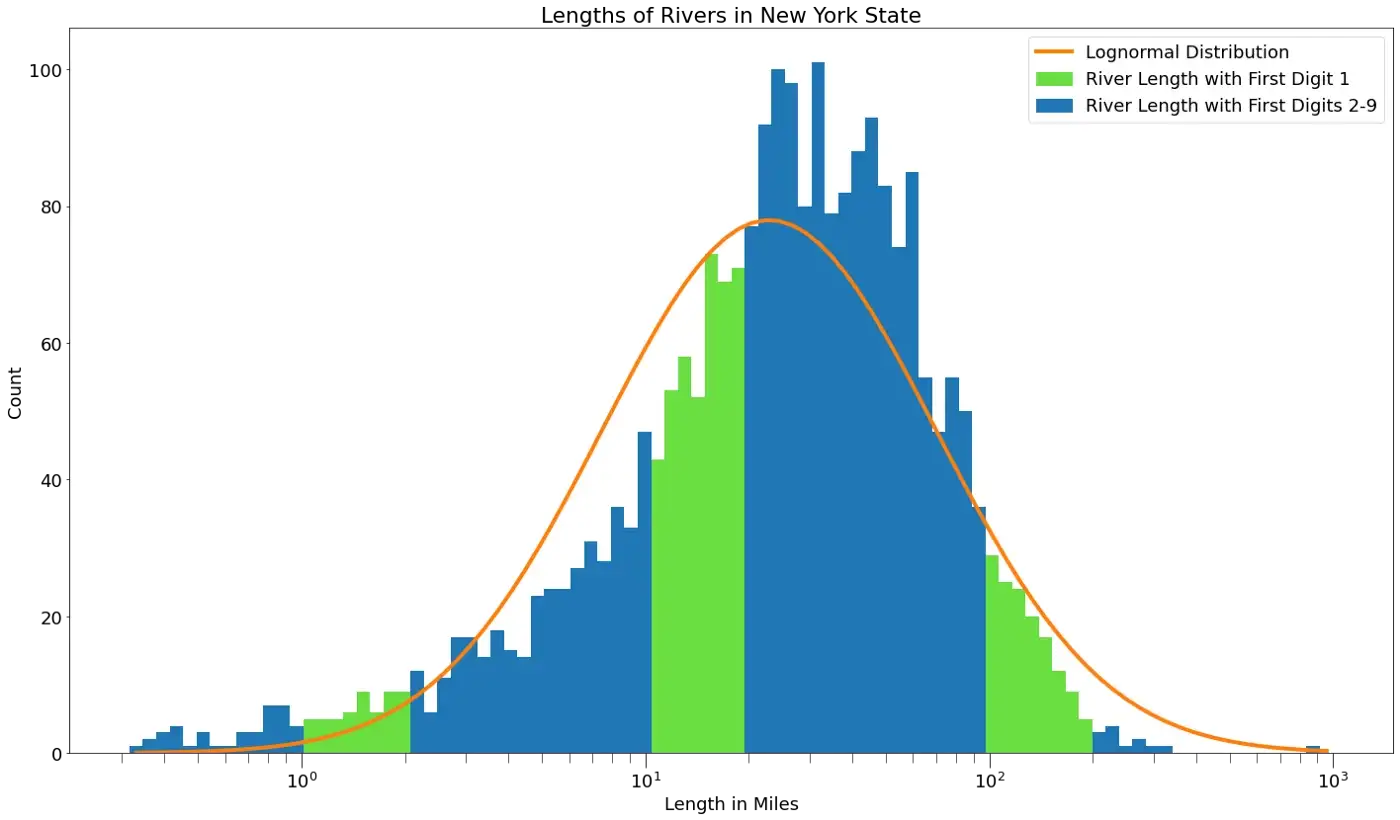
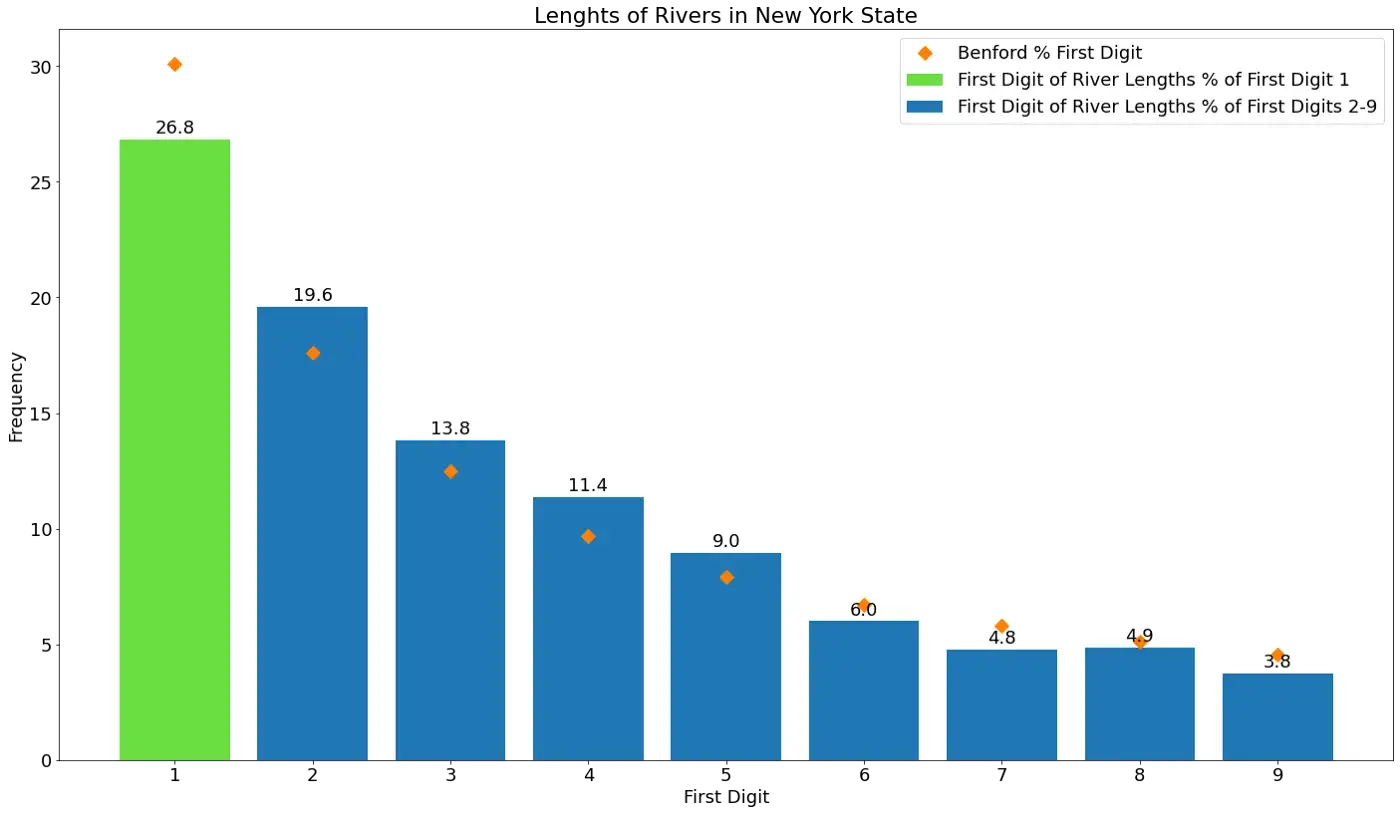
Desta vez, a distribuição está inclinada para a direita. Também podemos ver que os números com um dígito inicial de um estão abaixo da previsão da Lei de Benford. Isso é provavelmente devido ao fato de que o intervalo dinâmico, a relação entre o maior e o menor valor, não é muito grande. Há apenas três faixas verdes no histograma de distribuição, e nenhuma delas pega o pico da curva. Enquanto na população e exemplos de pagamentos acima vemos cinco e seis listras verdes respectivamente.
Por que a extensão dos rios segue uma distribuição log-normal? Alex Kossovsky tem uma explicação razoável. Ele afirma que …
“… o comprimento e a largura dos rios dependem da precipitação média (sendo o parâmetro) e a precipitação, por sua vez, depende das manchas solares, dos ventos predominantes e da localização geográfica, todos servindo como parâmetros de precipitação”.
– Alex Kossovsky
Espere, o quê? Manchas solares afetam a precipitação? Aparentemente sim, de acordo com a NASA [16]. Portanto, parece que a extensão dos rios é determinada por fatores múltiplos e independentes.
Há outros lugares na natureza onde podemos encontrar conjuntos de dados com distribuição log-normal. Por exemplo, Malcolm Sambridge, et al., exploram uma série de conjuntos de dados físicos em seu trabalho, “Benford’s Law in the Natural Sciences” [17]. Aqui está uma tabela de seu trabalho:
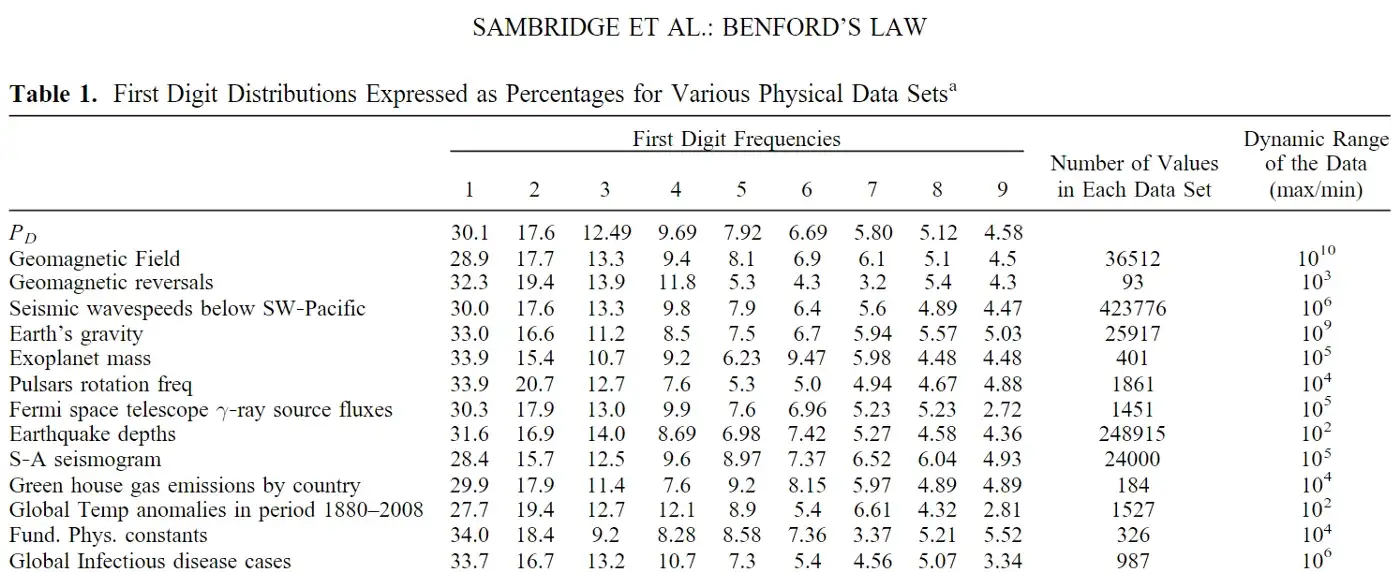
Você pode ver que estes conjuntos de dados seguem a Lei de Benford bastante de perto. Quanto ao porquê disto acontecer, Alex Kossovsky resume bastante bem [4]:
“Uma explicação plausível para a prevalência da Lei de Benford nas ciências naturais é que essas manifestações físicas da lei são obtidas através dos efeitos cumulativos de poucos ou muitos fatores aleatórios multiplicativos, o que leva à distribuição log-normal como a eventual distribuição…”
– Alex Kossovsky
Sumário
Neste artigo, dei uma visão geral da Lei de Benford, com algum contexto e história. Expliquei as distribuições normais e logaritmos com uma visão geral para entender as distribuições log-normais. Com alguns exercícios teóricos de lançamento de dados, mostrei como múltiplas variáveis independentes podem levar a distribuições normais (com adição) e log-normais (com multiplicação).
Além disso, mostrei como alguns conjuntos de dados com distribuições log-normais podem levar à conformidade com a Lei de Benford.
Por fim, examinei três exemplos de conjuntos de dados reais (populações de cidades/municípios, contas a pagar e extensão dos rios) para mostrar como os conjuntos de dados com distribuição log-normal tenderão a aderir à Lei de Benford.
Trabalho futuro
O trabalho futuro pode incluir a exploração de como os dois tipos de análises, a aderência às distribuições log-normais e a conformidade com a Lei de Benford podem estar relacionados quando os conjuntos de dados não correspondem aos ideais. Estas ferramentas em conjunto podem ajudar a determinar quaisquer razões subjacentes para quaisquer discrepâncias nos dados.
Agradecimentos
Gostaria de agradecer a Jennifer Lim e Matthew Conroy por sua ajuda e feedback sobre este projeto.
Código fonte
Todos os dados e código fonte para criar os gráficos deste artigo estão disponíveis no GitHub. As fontes são liberadas sob a licença CC BY-NC-SA.
Referências
[1] Netflix, Connected, 2020, https://www.netflix.com/title/81031737
[2] Scott, P. and Fasli, M., “CSM-349 – Benford’s Law: An Empirical Investigation and a Novel Explanation”, 2001, http://repository.essex.ac.uk/8664/1/CSM-349.pdf
[3] Berger, A., Hill, T.P., “A basic theory of Benford’s Law”, Probability Surveys, 2011, https://projecteuclid.org/download/pdfview_1/euclid.ps/1311860830
[4] Kossovsky A. E., “Arithmetical Tugs of War and Benford’s Law”, 2014, https://arxiv.org/ftp/arxiv/papers/1410/1410.2174.pdf
[5]Benford, F. “The Law of anomalous numbers”, Proceedings of the American Philosophical Society, 78, 551–572, 1938
[6] Newcomb, S., “Note on the frequency of use of different digits in natural numbers”, American Journal of Math. 4, 39–40, 1881
[7] Stigler S., “Stigler’s Law of Eponymy”, 1980, https://archive.org/details/sciencesocialstr0039unse/page/147/mode/2up
[8] Fewster, R.M., “A Simple Explanation of Benford’s Law”, The American Statistician, Vol. 63, No 1, 2009, https://www.stat.auckland.ac.nz/~fewster/RFewster_Benford.pdf
[9] US Census Data, 2010, https://www2.census.gov
[10] Decker, E. H., Kerkhoff, A. J., & Moses, M. E. (2007). Global patterns of city size distributions and their fundamental drivers. PloS one, 2(9), e934. https://doi.org/10.1371/journal.pone.0000934
[11] Nigrini, M.J., “I’ve Got Your Number”, Journal of Accountancy, 1999, https://www.journalofaccountancy.com/issues/1999/may/nigrini.html
[12] The state of Oklahoma, “Oklahoma’s Open Data”, https://data.ok.gov, 2019
[13] Durtschi, C., Hillison, W. Pacini C., “The effective use of Benford’s law to assist in detecting fraud in accounting data”, Journal of Forensic Accounting, 2004, http://lycofs01.lycoming.edu/~sprgene/M400/BenfordsLaw.pdf
[14] New York State, Waterbody Classifications, 2019, https://data.ny.gov/Energy-Environment/Waterbody-Classifications/8xz8-5u5u
[15] Kossovsky A. E., “Towards A Better Understanding of the Leading Digits Phenomena”, 2006, https://arxiv.org/ftp/math/papers/0612/0612627.pdf
[16] Rind, D., “Do Variations in the Solar Cycle Affect Our Climate System?” Science Briefs, Goddard Institute for Space Studies, NASA, 2009, https://www.giss.nasa.gov/research/briefs/2009_rind_03
[17] Sambridge S., Tkalčić H., and Jackson A., “Benford’s law in the natural sciences”, Geophysical Research Letters, Vol. 37, L22301, 2010, https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2010GL044830
* * * * *
Publicado originalmente em Towards Data Science em 2 de outubro de 2020.
Este conteúdo foi traduzido por Tiago Souza, com permissão do autor, Robert A. Gonsalves. O autor é um artista, inventor e engenheiro na área de Boston que pesquisa e escreve sobre os usos criativos de IA.




